2.4 神经网络的“引擎”:基于梯度的优化
上一节介绍过,我们的第一个神经网络示例中,每个神经层都用下述方法对输入数据进行变换。
output = relu(dot(W, input) + b)
在这个表达式中,W和b都是张量,均为该层的属性。它们被称为该层的权重(weight)或可训练参数(trainable parameter),分别对应kernel和bias属性。这些权重包含网络从观察训练数据中学到的信息。
一开始,这些权重矩阵取较小的随机值,这一步叫作随机初始化(random initialization)。当然,W和b都是随机的,relu(dot(W, input) + b)肯定不会得到任何有用的表示。虽然得到的表示是没有意义的,但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这个逐渐调节的过程叫作训练,也就是机器学习中的学习。
上述过程发生在一个训练循环(training loop)内,其具体过程如下。必要时一直重复这些步骤。
(1)抽取训练样本x和对应目标y组成的数据批量。
(2)在x上运行网络[这一步叫作前向传播(forward pass)],得到预测值y_pred。
(3)计算网络在这批数据上的损失,用于衡量y_pred和y之间的距离。
(4)更新网络的所有权重,使网络在这批数据上的损失略微下降。
最终得到的网络在训练数据上的损失非常小,即预测值 y_pred和预期目标y之间的距离非常小。网络“学会”将输入映射到正确的目标。乍一看可能像魔法一样,但如果你将其简化为基本步骤,那么会变得非常简单。
第一步看起来非常简单,只是输入 /输出(I/O)的代码。第二步和第三步仅仅是一些张量运算的应用,所以你完全可以利用上一节学到的知识来实现这两步。难点在于第四步:更新网络的权重。考虑网络中某个权重系数,你怎么知道这个系数应该增大还是减小,以及变化多少?
一种简单的解决方案是,保持网络中其他权重不变,只考虑某个标量系数,让其尝试不同的取值。假设这个系数的初始值为 0.3。对一批数据做完前向传播后,网络在这批数据上的损失是 0.5。如果你将这个系数的值改为 0.35并重新运行前向传播,损失会增大到 0.6。但如果你将这个系数减小到 0.25,损失会减小到 0.4。在这个例子中,将这个系数减小 0.05似乎有助于使损失最小化。对于网络中的所有系数都要重复这一过程。
但这种方法是非常低效的,因为对每个系数(系数很多,通常有上千个,有时甚至多达上百万个)都需要计算两次前向传播(计算代价很大)。一种更好的方法是利用网络中所有运算都是可微(differentiable)的这一事实,计算损失相对于网络系数的梯度(gradient),然后向梯度的反方向改变系数,从而使损失降低。
如果你已经了解可微和梯度这两个概念,可以直接跳到 2.4.3节。如果不了解,下面两小节有助于你理解这些概念。
2.4.1 什么是导数
假设有一个连续的光滑函数f(x) = y,将实数x映射为另一个实数y。由于函数是连续的,x的微小变化只能导致 y的微小变化——这就是函数连续性的直观解释。假设 x增大了一个很小的因子epsilon_x,这导致y也发生了很小的变化,即epsilon_y:
f(x + epsilon_x) = y + epsilon_y
此外,由于函数是光滑的(即函数曲线没有突变的角度),在某个点p附近,如果epsilon_x足够小,就可以将f近似为斜率为a的线性函数,这样epsilon_y就变成了a * epsilon_x:
f(x + epsilon_x) = y + a * epsilon_x
显然,只有在x足够接近p时,这个线性近似才有效。
斜率a被称为f在p点的导数(derivative)。如果a是负的,说明x在p点附近的微小变化将导致f(x)减小(如图 2-10所示);如果a是正的,那么x的微小变化将导致 f(x)增大。此外,a的绝对值(导数大小)表示增大或减小的速度快慢。
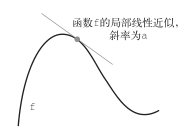
图 2-10 f在p点的导数
对于每个可微函数f(x)(可微的意思是“可以被求导”。例如,光滑的连续函数可以被求导),都存在一个导数函数f'(x),将x的值映射为f在该点的局部线性近似的斜率。例如,cos(x)的导数是-sin(x),f(x) = a * x的导数是f'(x) = a,等等。
如果你想要将x改变一个小因子epsilon_x,目的是将f(x)最小化,并且知道f的导数,那么问题解决了:导数完全描述了改变x后f(x)会如何变化。如果你希望减小f(x)的值,只需将x沿着导数的反方向移动一小步。
2.4.2 张量运算的导数:梯度
梯度(gradient)是张量运算的导数。它是导数这一概念向多元函数导数的推广。多元函数是以张量作为输入的函数。
假设有一个输入向量x、一个矩阵W、一个目标y和一个损失函数loss。你可以用W来计算预测值y_pred,然后计算损失,或者说预测值y_pred和目标y之间的距离。
y_pred = dot(W, x) loss_value = loss(y_pred, y)
如果输入数据x和y保持不变,那么这可以看作将W映射到损失值的函数。
loss_value = f(W)
假设W的当前值为W0。f在W0点的导数是一个张量gradient(f)(W0),其形状与W相同,每个系数gradient(f)(W0)[i, j]表示改变W0[i, j]时loss_value变化的方向和大小。张量gradient(f)(W0)是函数f(W) = loss_value在W0的导数。
前面已经看到,单变量函数f(x)的导数可以看作函数f曲线的斜率。同样,gradient(f)(W0)也可以看作表示f(W)在W0附近曲率(curvature)的张量。
对于一个函数 f(x),你可以通过将 x向导数的反方向移动一小步来减小 f(x)的值。同样,对于张量的函数 f(W),你也可以通过将 W向梯度的反方向移动来减小 f(W),比如W1 = W0 – step * gradient(f)(W0),其中step是一个很小的比例因子。也就是说,沿着曲率的反方向移动,直观上来看在曲线上的位置会更低。注意,比例因子 step是必需的,因为gradient(f)(W0)只是W0附近曲率的近似值,不能离W0太远。
2.4.3 随机梯度下降
给定一个可微函数,理论上可以用解析法找到它的最小值:函数的最小值是导数为 0的点,因此你只需找到所有导数为 0的点,然后计算函数在其中哪个点具有最小值。
将这一方法应用于神经网络,就是用解析法求出最小损失函数对应的所有权重值。可以通过对方程 gradient(f)(W) = 0求解W来实现这一方法。这是包含 N个变量的多项式方程,其中 N是网络中系数的个数。N=2或 N=3时可以对这样的方程求解,但对于实际的神经网络是无法求解的,因为参数的个数不会少于几千个,而且经常有上千万个。
相反,你可以使用 2.4节开头总结的四步算法:基于当前在随机数据批量上的损失,一点一点地对参数进行调节。由于处理的是一个可微函数,你可以计算出它的梯度,从而有效地实现第四步。沿着梯度的反方向更新权重,损失每次都会变小一点。
(1)抽取训练样本x和对应目标y组成的数据批量。
(2)在x上运行网络,得到预测值y_pred。
(3)计算网络在这批数据上的损失,用于衡量y_pred和y之间的距离。
(4)计算损失相对于网络参数的梯度[一次反向传播(backward pass)]。
(5)将参数沿着梯度的反方向移动一点,比如W -= step * gradient,从而使这批数据上的损失减小一点。
这很简单!我刚刚描述的方法叫作小批量随机梯度下降(mini-batch stochastic gradient descent,又称为小批量 SGD)。术语随机(stochastic)是指每批数据都是随机抽取的(stochastic是 random在科学上的同义词)。图 2-11给出了一维的情况,网络只有一个参数,并且只有一个训练样本。
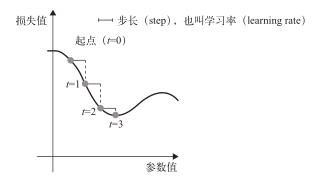
图 2-11 沿着一维损失函数曲线的随机梯度下降(一个需要学习的参数)
如你所见,直观上来看,为 step因子选取合适的值是很重要的。如果取值太小,则沿着曲线的下降需要很多次迭代,而且可能会陷入局部极小点。如果取值太大,则更新权重值之后可能会出现在曲线上完全随机的位置。
注意,小批量 SGD算法的一个变体是每次迭代时只抽取一个样本和目标,而不是抽取一批数据。这叫作真 SGD(有别于小批量 SGD)。还有另一种极端,每一次迭代都在所有数据上运行,这叫作批量 SGD。这样做的话,每次更新都更加准确,但计算代价也高得多。这两个极端之间的有效折中则是选择合理的批量大小。
图 2-11描述的是一维参数空间中的梯度下降,但在实践中需要在高维空间中使用梯度下降。神经网络的每一个权重参数都是空间中的一个自由维度,网络中可能包含数万个甚至上百万个参数维度。为了让你对损失曲面有更直观的认识,你还可以将梯度下降沿着二维损失曲面可视化, 如图 2-12所示。但你不可能将神经网络的实际训练过程可视化,因为你无法用人类可以理解的方式来可视化 1 000 000维空间。因此最好记住,在这些低维表示中形成的直觉在实践中不一定总是准确的。这在历史上一直是深度学习研究的问题来源。

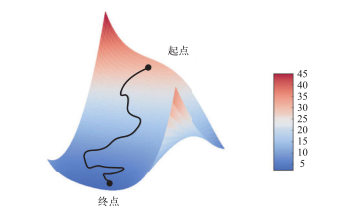
图 2-12 沿着二维损失曲面的梯度下降(两个需要学习的参数)
此外,SGD还有多种变体,其区别在于计算下一次权重更新时还要考虑上一次权重更新,而不是仅仅考虑当前梯度值,比如带动量的 SGD、Adagrad、RMSProp等变体。这些变体被称为优化方法(optimization method)或优化器(optimizer)。其中动量的概念尤其值得关注,它在许多变体中都有应用。动量解决了 SGD的两个问题:收敛速度和局部极小点。图 2-13给出了损失作为网络参数的函数的曲线。
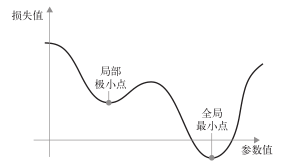
图 2-13 局部极小点和全局最小点
如你所见,在某个参数值附近,有一个局部极小点(local minimum):在这个点附近,向左移动和向右移动都会导致损失值增大。如果使用小学习率的 SGD进行优化,那么优化过程可能会陷入局部极小点,导致无法找到全局最小点。
使用动量方法可以避免这样的问题,这一方法的灵感来源于物理学。有一种有用的思维图像,就是将优化过程想象成一个小球从损失函数曲线上滚下来。如果小球的动量足够大,那么它不会卡在峡谷里,最终会到达全局最小点。动量方法的实现过程是每一步都移动小球,不仅要考虑当前的斜率值(当前的加速度),还要考虑当前的速度(来自于之前的加速度)。这在实践中的是指,更新参数w不仅要考虑当前的梯度值,还要考虑上一次的参数更新,其简单实现如下所示。

2.4.4 链式求导:反向传播算法
在前面的算法中,我们假设函数是可微的,因此可以明确计算其导数。在实践中,神经网络函数包含许多连接在一起的张量运算,每个运算都有简单的、已知的导数。例如,下面这个网络f包含 3个张量运算a、b和c,还有 3个权重矩阵W1、W2和W3。
f(W1, W2, W3) = a(W1, b(W2, c(W3)))
根据微积分的知识,这种函数链可以利用下面这个恒等式进行求导,它称为链式法则(chain rule):(f(g(x)))’ = f'(g(x)) * g'(x)。将链式法则应用于神经网络梯度值的计算,得到的算法叫作反向传播(backpropagation,有时也叫反式微分,reverse-mode differentiation)。反向传播从最终损失值开始,从最顶层反向作用至最底层,利用链式法则计算每个参数对损失值的贡献大小。
现在以及未来数年,人们将使用能够进行符号微分(symbolic differentiation)的现代框架来实现神经网络,比如 TensorFlow。也就是说,给定一个运算链,并且已知每个运算的导数,这些框架就可以利用链式法则来计算这个运算链的梯度函数,将网络参数值映射为梯度值。对于这样的函数,反向传播就简化为调用这个梯度函数。由于符号微分的出现,你无须手动实现反向传播算法。因此,我们不会在本节浪费你的时间和精力来推导反向传播的具体公式。你只需充分理解基于梯度的优化方法的工作原理。
2.5 回顾第一个例子
你已经读到了本章最后一节,现在应该对神经网络背后的原理有了大致的了解。我们回头看一下第一个例子,并根据前面三节学到的内容来重新阅读这个例子中的每一段代码。
下面是输入数据。
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))test_images = test_images.astype('float32') / 255
现在你明白了,输入图像保存在 float32格式的 Numpy张量中,形状分别为 (60000,784)(训练数据)和(10000, 784)(测试数据)。
下面是构建网络。
network = models.Sequential() network.add(layers.Dense(512, activation='relu',input_shape=(28 * 28,))) network.add(layers.Dense(10, activation='softmax'))
现在你明白了,这个网络包含两个Dense层,每层都对输入数据进行一些简单的张量运算,这些运算都包含权重张量。权重张量是该层的属性,里面保存了网络所学到的知识(knowledge)。
下面是网络的编译。
network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
现在你明白了,categorical_crossentropy是损失函数,是用于学习权重张量的反馈信号,在训练阶段应使它最小化。你还知道,减小损失是通过小批量随机梯度下降来实现的。梯度下降的具体方法由第一个参数给定,即rmsprop优化器。
最后,下面是训练循环。
network.fit(train_images, train_labels, epochs=5, batch_size=128)
现在你明白在调用fit时发生了什么:网络开始在训练数据上进行迭代(每个小批量包含128个样本),共迭代 5次[在所有训练数据上迭代一次叫作一个轮次(epoch)]。在每次迭代过程中,网络会计算批量损失相对于权重的梯度,并相应地更新权重。 5轮之后,网络进行了2345次梯度更新(每轮 469次),网络损失值将变得足够小,使得网络能够以很高的精度对手写数字进行分类。
到目前为止,你已经了解了神经网络的大部分知识。
本章小结
- 学习是指找到一组模型参数,使得在给定的训练数据样本和对应目标值上的损失函数最小化。
- 学习的过程:随机选取包含数据样本及其目标值的批量,并计算批量损失相对于网络参数的梯度。随后将网络参数沿着梯度的反方向稍稍移动(移动距离由学习率指定)。
- 整个学习过程之所以能够实现,是因为神经网络是一系列可微分的张量运算,因此可以利用求导的链式法则来得到梯度函数,这个函数将当前参数和当前数据批量映射为一个梯度值。
- 后续几章你会经常遇到两个关键的概念:损失和优化器。将数据输入网络之前,你需要先定义这二者。
- 损失是在训练过程中需要最小化的量,因此,它应该能够衡量当前任务是否已成功解决。
- 优化器是使用损失梯度更新参数的具体方式,比如 RMSProp优化器、带动量的随机梯度下降(SGD)等。

