3.6 预测房价:回归问题
前面两个例子都是分类问题,其目标是预测输入数据点所对应的单一离散的标签。另一种常见的机器学习问题是回归问题,它预测一个连续值而不是离散的标签,例如,根据气象数据预测明天的气温,或者根据软件说明书预测完成软件项目所需要的时间。
注意
不要将回归问题与 logistic回归算法混为一谈。令人困惑的是,logistic回归不是回归算法,而是分类算法。
3.6.1 波士顿房价数据集
本节将要预测 20世纪 70年代中期波士顿郊区房屋价格的中位数,已知当时郊区的一些数据点,比如犯罪率、当地房产税率等。本节用到的数据集与前面两个例子有一个有趣的区别。它包含的数据点相对较少,只有 506个,分为 404个训练样本和 102个测试样本。输入数据的每个特征(比如犯罪率)都有不同的取值范围。例如,有些特性是比例,取值范围为 0~1;有的取值范围为 1~12;还有的取值范围为 0~100,等等。
代码清单 3-24 加载波士顿房价数据
from keras.datasets import boston_housing (train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
我们来看一下数据。
>>> train_data.shape (404, 13) >>> test_data.shape (102, 13)
如你所见,我们有 404个训练样本和 102个测试样本,每个样本都有 13个数值特征,比如人均犯罪率、每个住宅的平均房间数、高速公路可达性等。
目标是房屋价格的中位数,单位是千美元。
>>> train_targets array([ 15.2, 42.3,50. ...19.4,19.4,29.1])
房价大都在 10 000~50 000美元。如果你觉得这很便宜,不要忘记当时是 20世纪 70年代中期,而且这些价格没有根据通货膨胀进行调整。
3.6.2 准备数据
将取值范围差异很大的数据输入到神经网络中,这是有问题的。网络可能会自动适应这种取值范围不同的数据,但学习肯定变得更加困难。对于这种数据,普遍采用的最佳实践是对每个特征做标准化,即对于输入数据的每个特征(输入数据矩阵中的列),减去特征平均值,再除以标准差,这样得到的特征平均值为 0,标准差为 1。用 Numpy可以很容易实现标准化。
代码清单 3-25 数据标准化
mean = train_data.mean(axis=0) train_data -= mean std = train_data.std(axis=0) train_data /= std test_data -= mean test_data /= std
注意,用于测试数据标准化的均值和标准差都是在训练数据上计算得到的。在工作流程中,你不能使用在测试数据上计算得到的任何结果,即使是像数据标准化这么简单的事情也不行。
3.6.3 构建网络
由于样本数量很少,我们将使用一个非常小的网络,其中包含两个隐藏层,每层有 64个单元。一般来说,训练数据越少,过拟合会越严重,而较小的网络可以降低过拟合。
代码清单 3-26 模型定义

网络的最后一层只有一个单元,没有激活,是一个线性层。这是标量回归(标量回归是预测单一连续值的回归)的典型设置。添加激活函数将会限制输出范围。例如,如果向最后一层添加sigmoid激活函数,网络只能学会预测 0~1范围内的值。这里最后一层是纯线性的,所以网络可以学会预测任意范围内的值。
注意,编译网络用的是mse损失函数,即均方误差(MSE,mean squared error),预测值与目标值之差的平方。这是回归问题常用的损失函数。
在训练过程中还监控一个新指标:平均绝对误差(MAE,mean absolute error)。它是预测值与目标值之差的绝对值。比如,如果这个问题的 MAE等于 0.5,就表示你预测的房价与实际价格平均相差 500美元。
3.6.4 利用 K折验证来验证你的方法
为了在调节网络参数(比如训练的轮数)的同时对网络进行评估,你可以将数据划分为训练集和验证集,正如前面例子中所做的那样。但由于数据点很少,验证集会非常小(比如大约100个样本)。因此,验证分数可能会有很大波动,这取决于你所选择的验证集和训练集。也就是说,验证集的划分方式可能会造成验证分数上有很大的方差,这样就无法对模型进行可靠的评估。
在这种情况下,最佳做法是使用 K折交叉验证(见图 3-11)。这种方法将可用数据划分为 K个分区(K通常取 4或 5),实例化 K个相同的模型,将每个模型在 K 1个分区上训练,并在剩下的一个分区上进行评估。模型的验证分数等于 K个验证分数的平均值。这种方法的代码实现很简单。
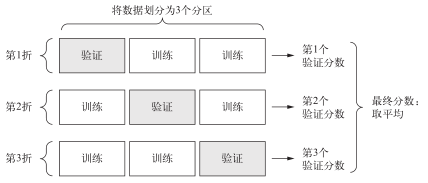
图 3-11 3折交叉验证
代码清单 3-27 K折验证

每次运行模型得到的验证分数有很大差异,从 2.6到 3.2不等。平均分数( 3.0)是比单一分数更可靠的指标——这就是 K折交叉验证的关键。在这个例子中,预测的房价与实际价格平均相差 3000美元,考虑到实际价格范围在 10 000~50 000美元,这一差别还是很大的。
我们让训练时间更长一点,达到 500个轮次。为了记录模型在每轮的表现,我们需要修改训练循环,以保存每轮的验证分数记录。
代码清单 3-28 保存每折的验证结果

然后你可以计算每个轮次中所有折 MAE的平均值。
代码清单 3-29 计算所有轮次中的 K折验证分数平均值
average_mae_history = [
np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]
我们画图来看一下,见图 3-12。
代码清单 3-30 绘制验证分数
import matplotlib.pyplot as plt
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
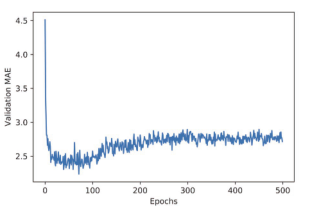
图 3-12 每轮的验证 MAE
因为纵轴的范围较大,且数据方差相对较大,所以难以看清这张图的规律。我们来重新绘制一张图。
- 删除前 10个数据点,因为它们的取值范围与曲线上的其他点不同。
- 将每个数据点替换为前面数据点的指数移动平均值,以得到光滑的曲线。
结果如图 3-13所示。
代码清单 3-31 绘制验证分数(删除前 10个数据点)
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()
从图 3-13可以看出,验证 MAE在 80轮后不再显著降低,之后就开始过拟合。
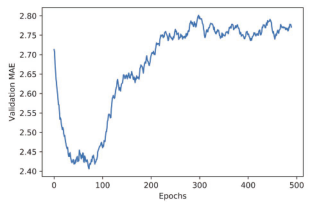
图 3-13 每轮的验证 MAE(删除前 10个数据点)
完成模型调参之后(除了轮数,还可以调节隐藏层大小),你可以使用最佳参数在所有训练数据上训练最终的生产模型,然后观察模型在测试集上的性能。
代码清单 3-32 训练最终模型

你预测的房价还是和实际价格相差约 2550美元。
3.6.5 小结
下面是你应该从这个例子中学到的要点。
- 回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差(MSE)。
- 同样,回归问题使用的评估指标也与分类问题不同。显而易见,精度的概念不适用于回归问题。常见的回归指标是平均绝对误差(MAE)。
- 如果输入数据的特征具有不同的取值范围,应该先进行预处理,对每个特征单独进行缩放。
- 如果可用的数据很少,使用 K折验证可以可靠地评估模型。
- 如果可用的训练数据很少,最好使用隐藏层较少(通常只有一到两个)的小型网络,以避免严重的过拟合。
本章小结
- 现在你可以处理关于向量数据最常见的机器学习任务了:二分类问题、多分类问题和标量回归问题。前面三节的“小结”总结了你从这些任务中学到的要点。
- 在将原始数据输入神经网络之前,通常需要对其进行预处理。
- 如果数据特征具有不同的取值范围,那么需要进行预处理,将每个特征单独缩放。
- 随着训练的进行,神经网络最终会过拟合,并在前所未见的数据上得到更差的结果。
- 如果训练数据不是很多,应该使用只有一两个隐藏层的小型网络,以避免严重的过拟合。
- 如果数据被分为多个类别,那么中间层过小可能会导致信息瓶颈。
- 回归问题使用的损失函数和评估指标都与分类问题不同。
- 如果要处理的数据很少,K折验证有助于可靠地评估模型。